Contrainte de cardinalité minimale 1 dans les associations 1:N
Rappel :
Méthode :
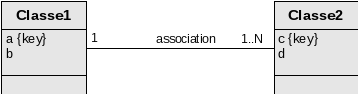
Si la cardinalité est exactement 1 (1..1) côté 1, alors on ajoutera une contrainte de non nullité sur la clé étrangère,
si la cardinalité est au moins 1 (1..N) côté N, on ajoutera une contrainte d'existence de tuples référençant pour chaque tuple de la relation référencée.
R1(#a,b)
R2(#c,d,a=>R1)
Contraintes : R2.a NOT NULL et PROJECTION(R1,a) = PROJECTION(R2,a)
On veut que tous les éléments de R1 soient référencés au moins une fois dans R2, donc il n'existe pas de tuple de R1 qui ne soit pas référencé par R2.a, donc PROJECTION(R1,a) = PROJECTION(R2,a).
#a | b |
|---|---|
1 | Lorem |
2 | Ipsum |
#c | b | a=>R1 |
|---|---|---|
a | Sed | 1 |
b | Ut | 2 |
c | Perspiciatis | 2 |
Complément : Cas général : PROJECTION(R1,a) ⊆ PROJECTION(R2,a)
Si la cardinalité côté 1 est 0..1 alors il peut exister la valeur NULL dans R2.a et donc la contrainte devient : PROJECTION(Classe1,a) ⊆ PROJECTION(Classe2,a).
#a | b |
|---|---|
1 | Lorem |
2 | Ipsum |
#c | b | a=>R1 |
|---|---|---|
a | Sed | 1 |
b | Ut | 2 |
c | Perspiciatis | 2 |
d | Unde | NULL |